Многочлен f(x+y)-f(x) делится на y без остатка (проверить по теореме Безу). Положим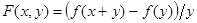 
. Многочлен F(x,0) называют производной многочлена f(x) и обозначают 
.
Теорема 2.14 (Свойства производной)
1. 
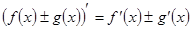
2. 
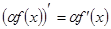
3. 
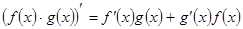
Доказательство следует из определения производной.
Говорят, что кратность корня a многочлена f(x) равна k, если f(x) делится на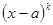 
и не делится (без остатка) на 
.
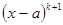Теорема 2.15 (Кратность корня)
Если a корень многочлена f(x) кратности k, то a корень его производной кратности k-1.
Доказательство. Пусть a корень кратности k многочлена f(x). Тогда f(x) представим в виде произведения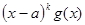 
, причём 
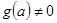. Производная от f(x) равна 
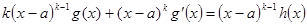, где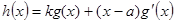 
. Поскольку 
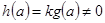, то теорема доказана.
Следствие 2.6 Многочлен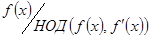 
не имеет кратных множителей.
Доказательство. Перейдём к полю разложения f(x). Многочлен 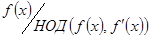над этим полем имеет те же самые корни, что и f(x), только кратности 1. Вернёмся в исходное поле P. Многочлен 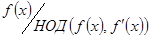разлагается на те же неприводимые множители что и f(x), только кратности 1.
