Многочлен называется неприводимым над числовым полем, если он не делится на многочлены меньшей степени (исключая константы)
Теорема 2.7 Пусть многочлен f(x) неприводим. Тогда
I. Из 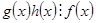 вытекает, либо
вытекает, либо 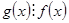 , либо
, либо 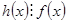 .
.
II. Если неприводимый многочлен делится на неприводимый многочлен, то они отличаются числовым множителем.
Доказательство.
Докажем первое утверждение. Если 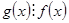 , то утверждение верно. Пусть
, то утверждение верно. Пусть 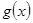 не делится на
не делится на 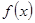 , тогда
, тогда  и найдутся многочлены
и найдутся многочлены 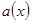 и
и 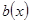 , что
, что 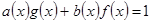 . Умножим полученное равенство на
. Умножим полученное равенство на 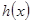 :
: 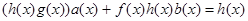 . В левой части равенства все слагаемые делятся на
. В левой части равенства все слагаемые делятся на 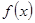 , следовательно,
, следовательно, 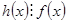 .
.
Второе утверждение следует непосредственно из определения неприводимого многочлена.
Теорема 2.8 Многочлен над числовым полем единственным образом раскладывается в произведение неприводимых многочленов, с точностью до перестановки сомножителей и числовых множителей.
Доказательство проведём индукцией по числу сомножителей. Если многочлен имеет один сомножитель, то он неприводим, и теорема верна. Пусть теорема верна для любого многочлена, разлагающегося на не более n-1 сомножителей. Допустим, найдётся многочлен, имеющий как минимум два разложения на неприводимые множители 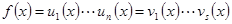 (
( 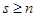 ). Поскольку произведение
). Поскольку произведение 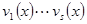 делится на
делится на 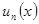 , то найдётся номер i, что
, то найдётся номер i, что  делится на
делится на 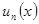 . Переставим сомножители так, чтобы i=s. Многочлены
. Переставим сомножители так, чтобы i=s. Многочлены 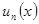 и
и 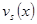 отличаются числовым множителем
отличаются числовым множителем 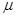 . Следовательно,
. Следовательно, 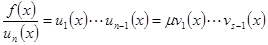 . По предположению индукции s-1=n-1 и сомножители отличаются только порядком и числовыми коэффициентами. Теорема доказана.
. По предположению индукции s-1=n-1 и сомножители отличаются только порядком и числовыми коэффициентами. Теорема доказана.