1.7.3.1 Вычисление формул вида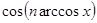 
Введём комплексное число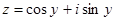 
. Из формулы Муавра-Лапласа вытекают равенства 
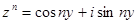и 
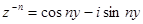, сложив их, получим 
. Из последнего равенства выводим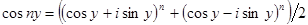 
, и далее по биному Ньютона 
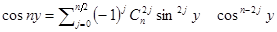. Положив 
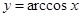, придём к равенству 
.
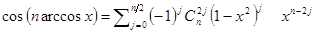1.7.3.2 Вычисление формул вида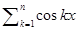 
Введём комплексное число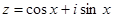 
. Как и выше, выводим 
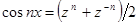. Подставим в сумму 
. Для выполнения операции деления представим 1-z в тригонометрической форме: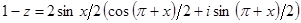 
и аналогично 
. После выполнения преобразований придём к окончательной формуле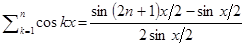 
1.7.3.3 Вычисление формул вида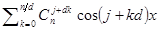 
.
Обозначим сумму через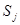 
, где j=0,1,…,d-1, а через 
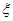- первообразный корень степени d из 1. Тогда, легко проверить, 
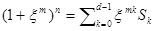, где j=0,1,…,d-1. Умножим каждое из равенств на 
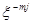и сложим. В результате получим равенство 
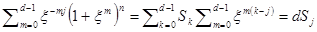. Запишем 
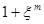в тригонометрической форме 
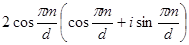возведём в степень n и подставим: 
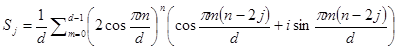или, что 
.
