Из комплексного числа существует ровно n корней степени n. Справедливо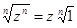 
. Если 
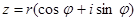, то множество всех корней n-ой степени имеет вид: 
.
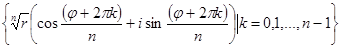Отсюда вытекает, что формула Муавра-Лапласа обобщается и на случай рациональных степеней. Следует иметь в виду, что она даёт одно из возможных значений, а не всё множество.
Особый интерес представляет множество корней степени n из 1. Легко проверить, что это множество замкнуто относительно операции умножения. Более того, множество корней степени n представляется как степень одного из корней, т.е.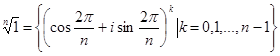 
. Корень степени n из 1 называется первообразным, если последовательным возведением его в степень можно получить всё множество корней степени n из 1.
Теорема 1.5 (о первообразных) Корень из 1 вида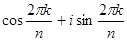 
является первообразным тогда и только тогда, когда наибольший общий делитель k и n равен 1.
Доказательство. Положим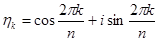 
и построим последовательность чисел 
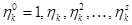до первого повторения. Поскольку в указанной последовательности встречаются только корни из 1 степени n, количество которых не больше n, то повтор наступит обязательно. Пусть 
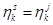и j>1, тогда 
, и повтор встретился раньше. Следовательно, s - наименьшее число, при котором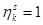 
, или, то же самое, ks делится на n без остатка. Наименьшее число s, при котором ks делится на n, равно n/НОД(n,k). Корень 
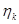будет первообразным тогда и только тогда, когда в последовательности встречаются все корни, т.е. s=n, а значит n=n/НОД(n,k), или НОД(n,k)=1.
