С многочленами над числовым кольцом можно проводить операции сложения, вычитания и умножения. Данные операции разобраны в школьном курсе математики. Ясно, что в результате получится многочлен с коэффициентами из этого же кольца. Интересна связь коэффициентов произведения многочленов с коэффициентами сомножителей. Пусть в результате перемножения многочленов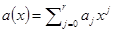 
и 
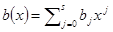получается многочлен 
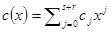. Тогда 
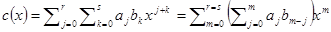, в правой части равенства предполагается, что 
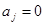при 
и 
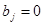при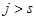 
.
Над многочленами над числовым полем кроме перечисленных операций определена операция деления с остатком.
Теорема 2.1 (Деление многочленов)
При делении многочленов над некоторым полем частное и остаток определены единственным образом.
Доказательство очевидно.
Для деления на двучлен x-a разработана компактная схема деления, которая называется схемой Горнера. Данная схема применяется и для вычислений значения многочлена в точке.
Теорема 2.2 (Безу)
Остаток от деления многочлена f(x) на двучлен x-a равен f(a).
