Комплексному числу c поставим в соответствие точку плоскости c координатами (Re(c),Im(c)). Это соответствие взаимно однозначное. Для вектора, соединяющего начало координат, с этой точкой определено понятие длины и угла с осью, по которой откладывается вещественная часть. Длину вектора называют модулем комплексного числа и обозначают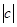 
, а угол называют аргументом комплексного числа и обозначают Arg(c). Имеют место соотношения 
, 
, 
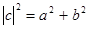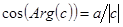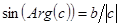. Из них получаем тригонометрическую форму комплексного числа 
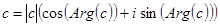. Данная форма полезна при вычислении произведения и частного комплексных чисел.
Теорема 1.3 Пусть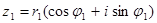 
и 
, тогда 
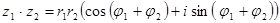и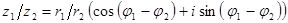 
.
Доказательство теоремы вытекает из тригонометрических тождеств и правил проведения соответствующих операций над комплексными числами в алгебраической форме.
Из данной теоремы вытекает
Теорема 1.4 (Формула Муавра-Лапласа) Для целого n и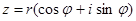 
справедливо 
.
