Множество чисел, замкнутых относительно операции +, *, и в котором разрешимо уравнение a+x=b называется числовым кольцом.
Любое числовое кольцо содержит 0.
Множество чётных чисел - кольцо без 1
Числовое кольцо, в котором разрешимо уравнение ax=b (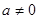 
) называется числовым полем.
Теорема 1.2 В любом числовом поле содержится поле рациональных чисел.
Доказательство. Пусть 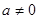- элемент этого поля. Тогда 
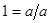принадлежит полю, а значит в силу замкнутости относительно операции + и все натуральные числа. Поскольку уравнение a+x=b разрешимо для всех элементов поля, то в нём содержатся все целые числа. Аналогично, из разрешимости уравнения ax=b вытекает, что в поле содержатся все рациональные числа.
Кроме поля рациональных чисел существуют другие поля. Например: числа вида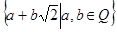 
образуют числовое поле.
