Этот способ является частным случаем способа плоскопараллельного перемещения, когда точка фигуры описывает дугу окружности, плоскость которой также параллельна плоскости проекций.
Графический алгоритм построения точек в способе вращения вокруг проецирующей прямой отличается лишь тем, что здесь траектория движения точки имеет вид окружности, а не произвольной прямой, как в плоскопараллельном проецировании.
Способ вращения вокруг проецирующей прямой более удобен при решении некоторых задач. Найдем с применением этого метода длину отрезка AB. Отрезок AB спроецируется на П2 в натуральную величину, если он будет ей параллелен. Для этого повернем его вокруг оси, проходящей через точку B до состояния параллельности П2, при этом точка A опишет дугу в горизонтальной плоскости.
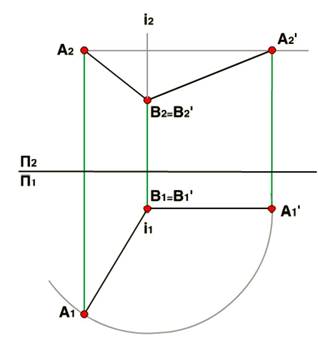
Алгоритм графических построений:
1.Проведем ось вращения i через точку B. Ось i перпендикулярна П2;
2.Повернем отрезок AB до состояния параллельности оси проекций П1П2. Где A1'B1' - новая проекция AB;
3.Проводим вспомогательную линию на П2. Эта линия символизирует горизонтальную плоскость, в которой поворачивалась точка A;
4.Проводим линию связи и находим новую проекцию A2'B2' отрезка AB на П2;
A2'B2' - натуральная величина отрезка AB.