|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
РЯДЫ ТЕЙЛОРА И МАКЛОРЕНАДата добавления: 2014-09-25; просмотров: 2638; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

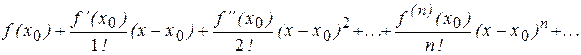
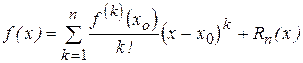 ,
, , x заключено между х0 и х.
, x заключено между х0 и х.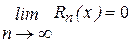 .
.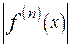 < M (nÎN ).
< M (nÎN ).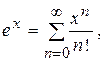
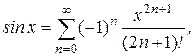
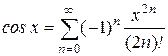 (по определению 0!=1).
(по определению 0!=1).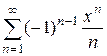 ,
,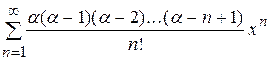 .
. За приближенное значение функции берется n-ая частичная сумма ряда Маклорена. При этом остаточный член ряда представляет собой абсолютную ошибку вычислений. Оценка остатка позволяет определить требуемое число слагаемых в частичной сумме. и для знакочередующегося ряда проводится на основании признака Лейбница ( абсолютная величина остатка ряда не превосходит абсолютной величины первого из отбрасываемых членов ряда).
За приближенное значение функции берется n-ая частичная сумма ряда Маклорена. При этом остаточный член ряда представляет собой абсолютную ошибку вычислений. Оценка остатка позволяет определить требуемое число слагаемых в частичной сумме. и для знакочередующегося ряда проводится на основании признака Лейбница ( абсолютная величина остатка ряда не превосходит абсолютной величины первого из отбрасываемых членов ряда).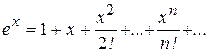
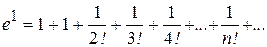
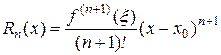 .
.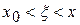 .
. 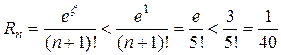 ,
, 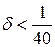 .
.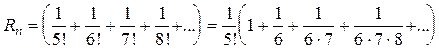 <
<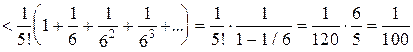 .
.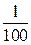 т.е. после запятой оставляем две верные цифры
т.е. после запятой оставляем две верные цифры с точностью 0,0001.
с точностью 0,0001.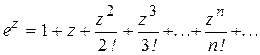 .
.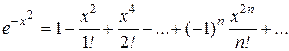 , xÎ(-¥,+¥).
, xÎ(-¥,+¥).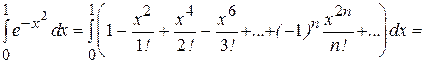

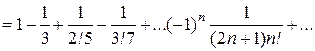
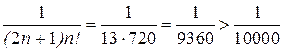 ,
,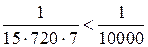 .
.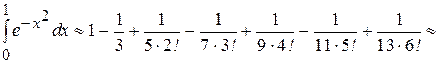
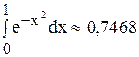 .
.