1) Если ряд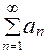 
сходится, то сходится и ряд, полученный отбрасыванием из него или изменением любого конечного числа членов.
2) Пусть даны ряды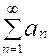
,
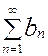и 
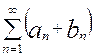. Если оба ряда 
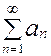и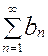 
сходятся, а их суммы соответственно равны A и B, то сходится и ряд
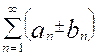, причем его сумма равна A 
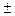B.
3) Если ряд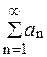 
сходится и имеет сумму А, то сходится и ряд 
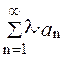, причем его сумма равна числу l×А, где l = const.
4) Если ряд 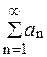сходится, то сходится и любой ряд, полученный из него группировкой слагаемых, не изменяющей порядок расположения членов ряда, и суммы этих рядов одинаковы. К примеру, если 
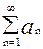сходится и его сумма равна А, то ряд
(a1 + a2) + (a3 + a4) + ... + (a 2n-1 + a 2n) + ...
также сходится, и его сумма равна А.
