Определение.Функция 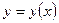 называется неявно заданной, если она задана с помощью уравнения называется неявно заданной, если она задана с помощью уравнения 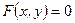 , не разрешенного относительно « , не разрешенного относительно « 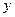 ». ».
ТЕОРЕМА.
Пусть функция 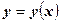 задана неявно при помощи уравнения задана неявно при помощи уравнения 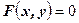 . Предположим, что: . Предположим, что:
1) 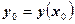 , т.е. , т.е. 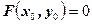 ; ;
2) существуют 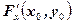 и и 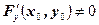 . .
Тогда:
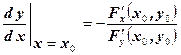 . .
Замечание.
Рассмотрим функцию двух переменных 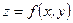 , заданную неявно уравнением: , заданную неявно уравнением:
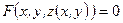 . .
Тогда при определенных условиях в некоторой точке 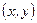 : :
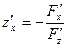 , , 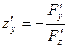 . .
Пример 4. Рассмотрим функцию 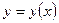 , заданную неявно уравнением: , заданную неявно уравнением: 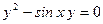 . .
Здесь 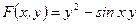 . Найдем . Найдем 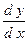 в некоторой точке в некоторой точке 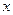 . Вычислим . Вычислим 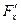 , , 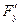 : :
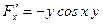 , , 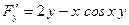 . .
Тогда:
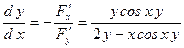 . .
Пример 5. Рассмотрим функцию 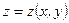 , заданную неявно уравнением: , заданную неявно уравнением: 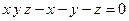 . .
Здесь  . Найдем . Найдем 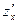 и и 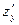 в некоторой точке в некоторой точке 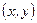 . Вычислим . Вычислим 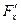 , , 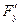 , , 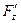 . .
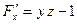 , , 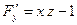 , , 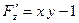 . .
Поэтому:
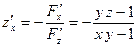 , , 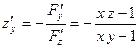 . .
Задачи для самостоятельного решения
1) 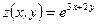 , , 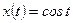 , , 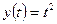 . Найти . Найти 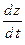 ; ;
2) 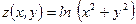 , , 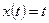 , , 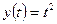 . Найти . Найти 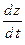 ; ;
3) 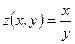 , , 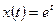 , , 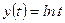 . Найти . Найти 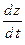 ; ;
4) 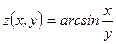 , , 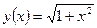 . Найти . Найти 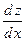 ; ;
5)  , , 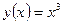 . Найти . Найти 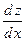 ; ;
6) 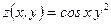 , , 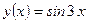 . Найти . Найти 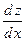 ; ;
7) 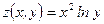 , , 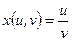 , ,  . Найти . Найти 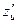 , , 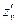 ; ;
8) 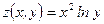 , , 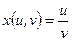 , , 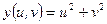 . Найти . Найти 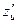 , , 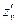 ; ;
9) 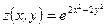 , , 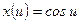 , , 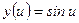 . Найти . Найти 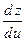 ; ;
10) 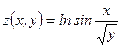 , , 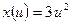 , , 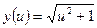 . Найти . Найти 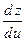 ; ;
11) 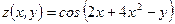 , , 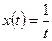 , ,  . Найти . Найти 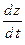 ; ;
12) 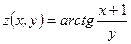 , ,  . Найти . Найти 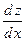 ; ;
13) 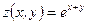 , , 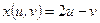 , , 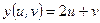 . Найти . Найти 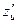 , , 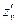 ; ;
14) 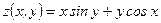 , , 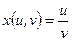 , , 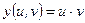 . Найти . Найти 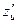 , , 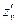 ; ;
15) 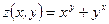 , , 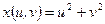 , , 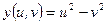 . Найти . Найти 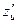 , , 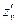 ; ;
16) 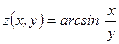 , , 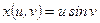 , ,  . Найти . Найти 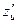 , , 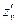 . .
В задачах 17) – 22) найти производную 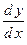 неявно заданной функции неявно заданной функции 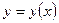 . .
17) 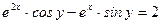 ; ;
18) 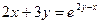 ; ;
19) 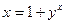 ; ;
20) 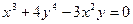 ; ;
21) 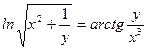 ; ;
22) 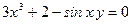 . .
В задачах 23) – 25) найти 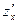 , , 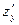 неявно заданной функции неявно заданной функции 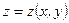 . .
23) 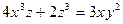 ; ;
24) 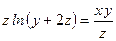 ; ;
25) 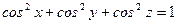 . .
|