С помощью рядов Тейлора и Маклорена можно приближенно вычислять значения функций. Для этого функцию раскладывают в степенной ряд Тейлора и заменяем сумму ряда его частичной суммой. Возникающую при этом погрешность (остаточный член) оценивают следующим образом:
1) если ряд знакочередующийся, то последствию из теоремы Лейбница, для знакочередующихся рядов, остаточный член не превосходит модуля 1 отбрасываемого члена.
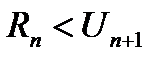
2) если ряд знакоположительный, то остаточный член оценивается непосредственно.