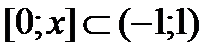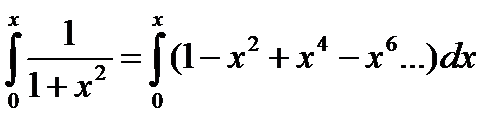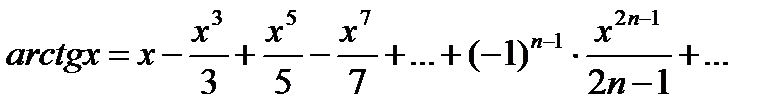Если в ряде Тейлора 
, то получим ряд Маклорена по степеням х.
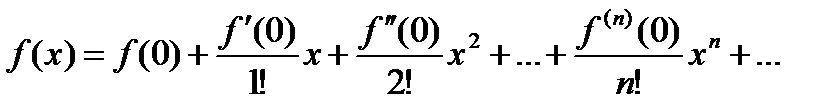
Остаточный член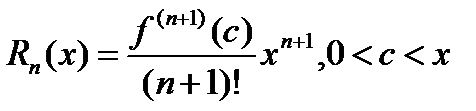 
Получим разложение некоторых элементарных функций в ряд Маклорена и найдём интервалы сходимости этих рядов.
1)
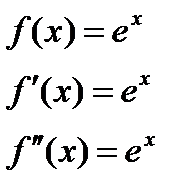
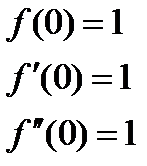
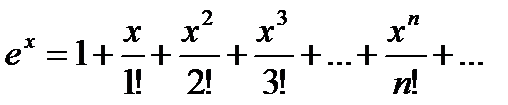Интервал сходимости этого ряда найдем непосредственно по признаку Даламбера.
Интервал сходимости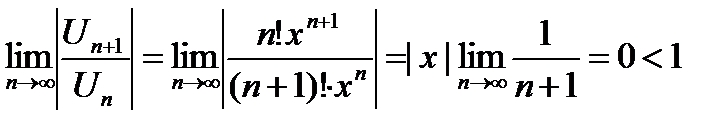 
При любом х ряд сходится по признаку Даламбера.
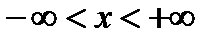- интервал сходимости.
2)
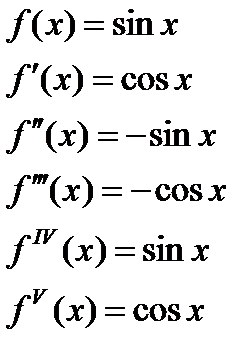
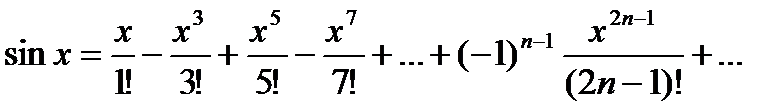
т.к семейство производных любого порядка равномерно ограничено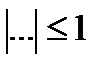 
при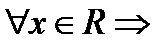 
интервал сходимости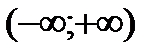 
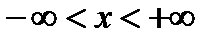
3)
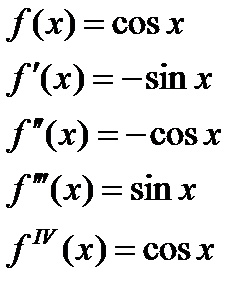
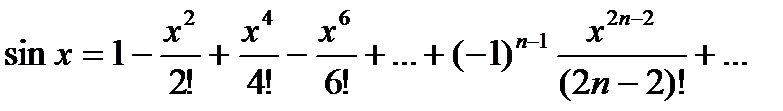
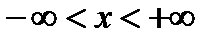- интервал сходимости.
4) Биномиальное разложение
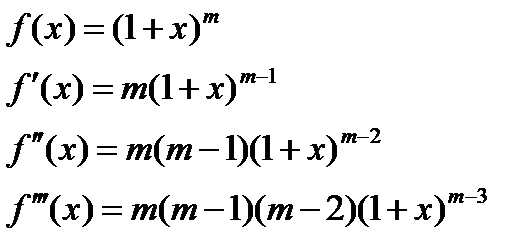
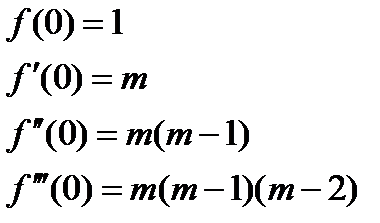
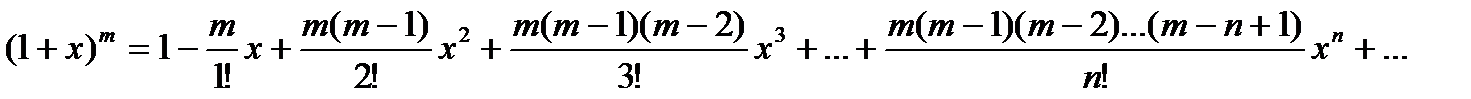
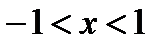- интервал сходимости.
5) f(x)=ln(1+x)
Воспользуемся предыдущим биномиальным разложением:
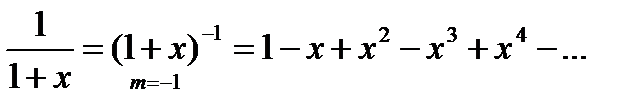
проинтегрируем почленно на отрезке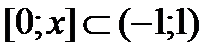 
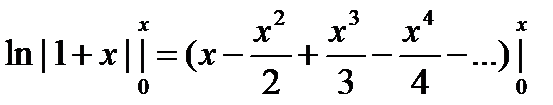
снимем модуль, т.к 1+х>0
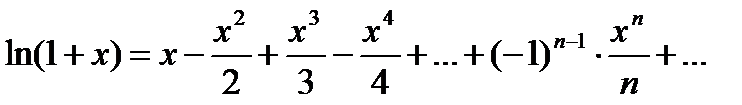
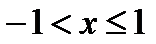- можно показать.
6) f(x)=arctgx
воспользуемся биномиальным разложением и заменим 
проинтегрируем на
