Дано 2 ряда с положительными членами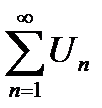 
(1) и 
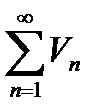(2) и 
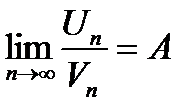- число 
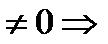(1) и (2) сходятся и расходятся одновременно.
Доказательство:
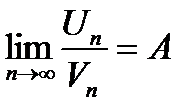- число 
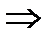по определению предела последовательности:
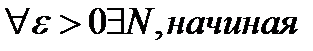с которого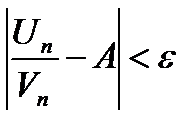 
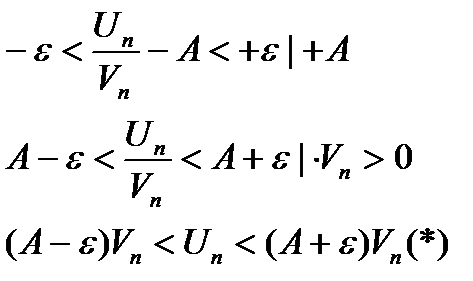
Пусть (2) сходится , тогда сходится и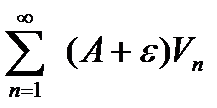 
Из правой части 
следует, что (1) ряд меньше сходящегося ряда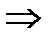 
по 1 признаку сравнения 
(1) сходится.
Пусть (2) расходится 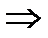выберем 
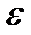настолько малым, чтобы 
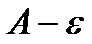оставалось >0, для знакоположительности ряда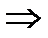 
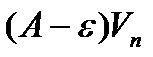- расходится. Из левой части (*) (1) ряд>ряда расходящегося по I признаку сравнения (1) ряд расходится.
Конец доказательства.
