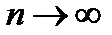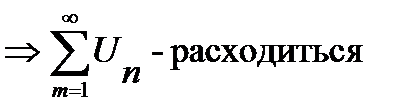Признаки сходимости.

Необходимый признак сходимости:

Если 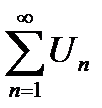сходится, то общий член

Доказательство: Пусть 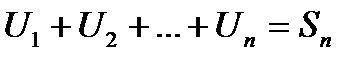- n – частичная сумма.

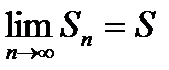- число.

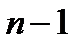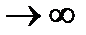При , тоже и 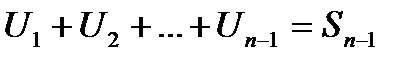- n-1 – частичная сумма.

Она имеет предел .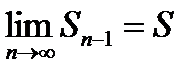

Т.к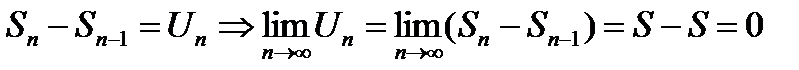

конец доказательства.

Необходимый признак сходимости неудобен на практике, т.к по поведению общего члена U_n на бесконечности нельзя судить о сходимости ряда.

На практике удобно пользоваться достаточным признаком расходимости ряда:

Если 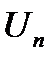не стремится к 0 при