Рассмотрим систему дифференциальных уравнений:
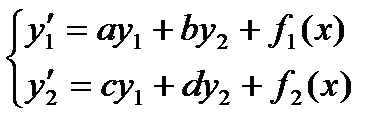, где a,b,c,d – числа.
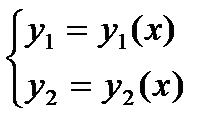- искомая функция 
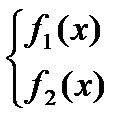- функции переменной х
продифференцируем по переменной х первое уравнение системы:
(1) 
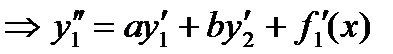
Подставим из (2)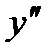 
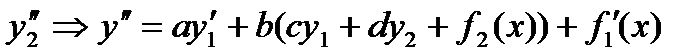
подставим из (1) 
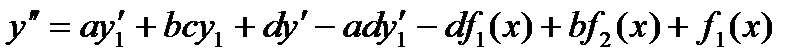
перенесем слагаемые с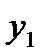 
и 
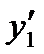налево
получим линейное неоднородное дифференциальное уравнение 2 порядка с постоянными коэффициентами. Решая это уравнение получим 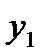, продифференцируем 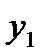и найдём 
.
Числовые ряды.
Определение:Рассмотрим бесконечную числовую последовательность:
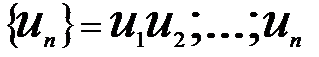числовым рядом называется выражение 
, где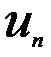 
– общий член ряда.
Пример:
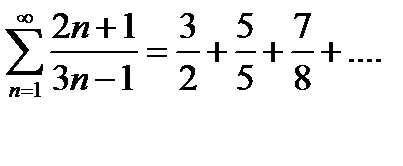-знакоположительный ряд
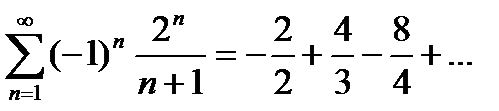-знакочередующийся ряд
Последовательность 
, где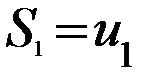 
; 
; 
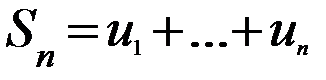- последовательность частичных сумм ряда.
Каждая частичная сумма содержит конечное число слагаемых.
Числовой ряд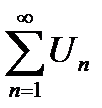 
называется сходящимся, если существует конечный
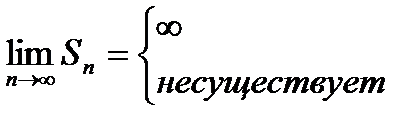, то ряд называется расходящимся и суммы S не имеют.
1)Рассмотрим ряд из членов геометрической прогрессии.
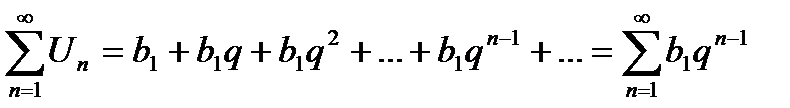, где n – частичная сумма ряда 
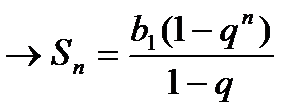- сумма n первых членов геометрической прогрессии.
Рассмотрим 3 случая:
1) 
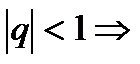геометрическая прогрессия убывающая.
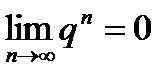
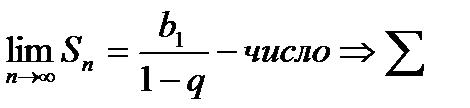сходится и имеет сумму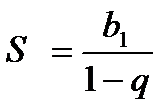 
2) 
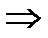
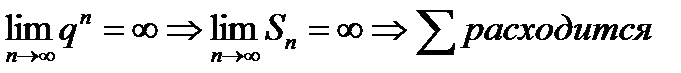
3) 
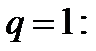
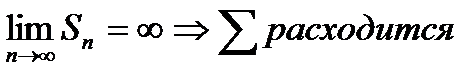
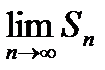= не существует – ряд расходится.
Вывод: ряд из членов геометрической прогрессии сходится если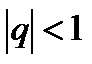 
и расходится 
.
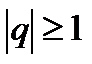