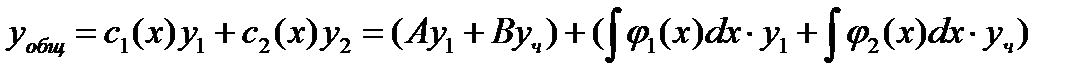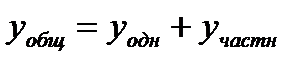Рассмотрим дифференциальное уравнение: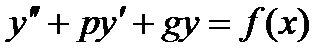 
Где правая часть f(x) произвольного вида (необязательно специального).
Общее решение соответствующего однородного уравнения:
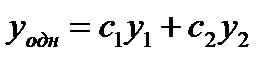, где 
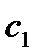и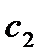 
- произвольные const, 
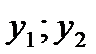- ФСР.
Будем варьировать 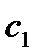и 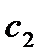и считать, что 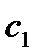и 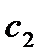зависит от х. Будем искать общее решение неоднородного уравнения (исходного) в виде:
(*)
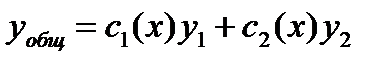
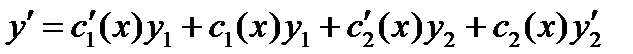
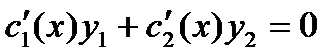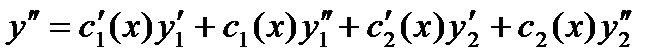
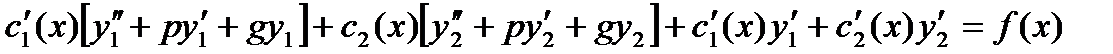
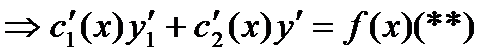
объединим 
и 
в систему
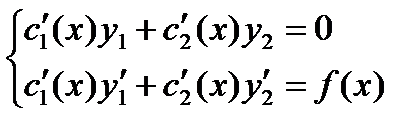- эта система для нахождения 
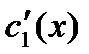и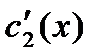 
имеет единственное решение, т.к определитель системы 
,
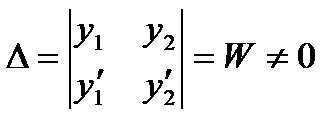для системы 2-х ЛНЗ надежнее решать систему по формулам Крамера
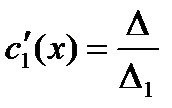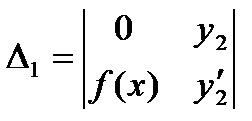
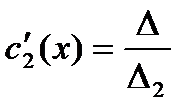, где 
, где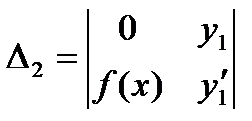 
решая систему получим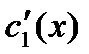 
и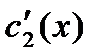 
, проинтегрируем полученные функции по переменной х.
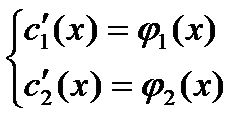- проинтегрируем по х
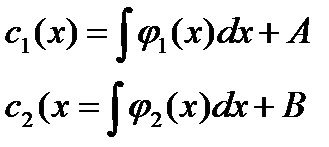, где А и В – константы интегрирования
Таким образом общее решение неоднородного уравнения:
