Это уравнения вида: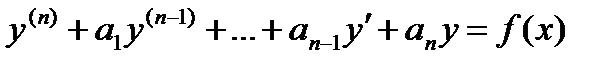 
Теорема об общем решении:Общее решение ДУ(*) имеет вид:
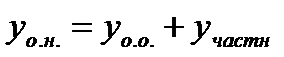, где 
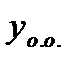- общее решение соответствующего однородного уравнения.
Доказательство: подставим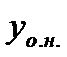 
в 
раскроем скобки и перегруппируемся:
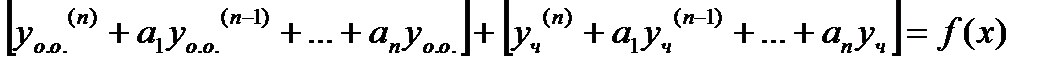(верно)
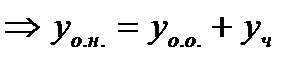
Если даны н.у
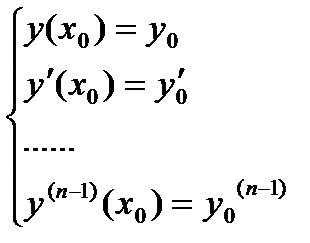
нужно показать, что все константы находятся однозначно
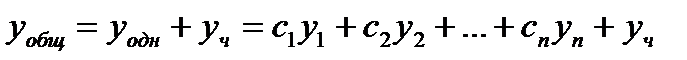, где ФСР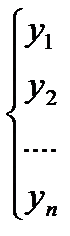 
Продифференцируем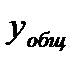 
нужное количество раз и подставим н.у
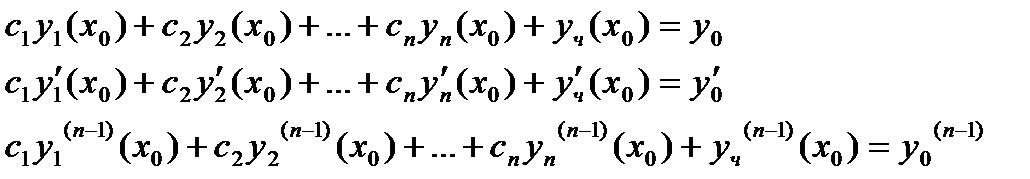
получим систему n-линейных уравнений с n неизвестными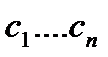 
. Определитель этой системы 
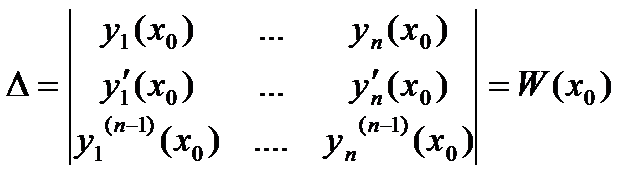- определитель Вронского системы функций 
.
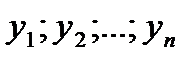Т.к 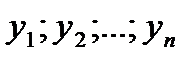- ФСР 
линейная система имеет единственное решение и все константы находятся однозначно.
Конец доказательства.
Замечание:Общее решение соответствующего однородного уравнения
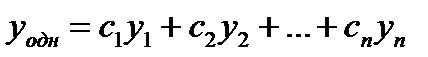- линейная комбинация ФСР – известно
Основная трудность нахождения yч – решения неоднородного уравнения.
