Линейные однородные дифференциальные уравнения порядка n.

Уравнение вида: 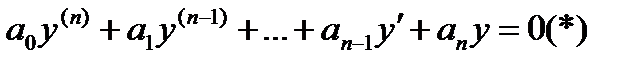называются линейными однородными дифференциальными уравнениями порядка n.

Для этих уравнений справедливы следующие теоремы:

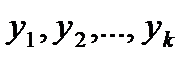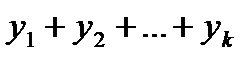Теорема 1:Если - решение , то сумма - тоже решение

Доказательство: подставим сумму в

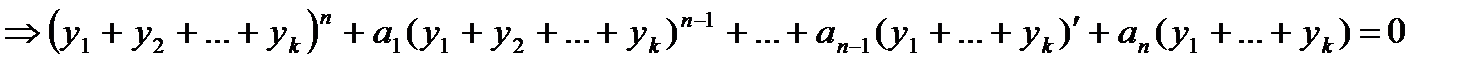
Т.к производная любого порядка от суммы равна суме производных, то можно перегруппироватся , раскрыв скобки:

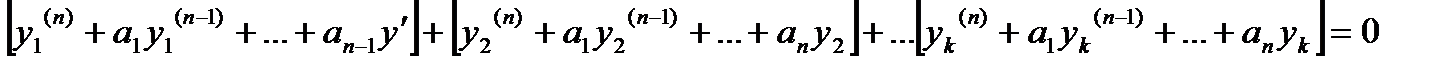
т.к y₁ и y₂ – решение.

0=0(верно) 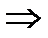сумма тоже решение.

теорема доказана.

Теорема 2:Если y₀-решение , то 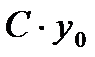- тоже решение .

Доказательство: Подставим 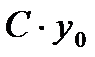в уравнение

т.к С выносится за знак производной, то

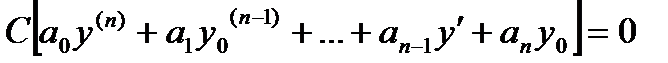
т.к 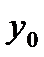решение, 0=0(верно) 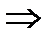Сy₀-тоже решение.

теорема доказана.

Следствие из Т1 и Т2:если 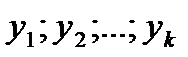- решения (*) линейеая комбинация -тоже решение (*).