Самый простой способ – линейная интерполяция – состоит в приближенной замене изучаемой функции на линейную функцию, причем так, чтобы обе функции совпадали при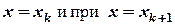 
(рис. 2.8).
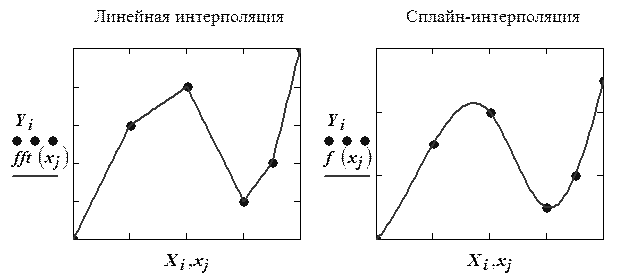
Рис. 2.8. Линейная и сплайновая интерполяция
Формула линейной интерполяции: 
. Графически это означает простое соединение узловых точек отрезками прямых.
Большую точность может дать квадратичная интерполяция, при которой изучаемая функция приближенно заменяется на квадратичную, причем так, чтобы обе функции совпадали при 
и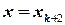 
.
Формула Ньютона для квадратичной интерполяции (рис. 2.9.а):
.
Данная формула не симметрична – в ней использованы значения 
.
Если обратить направление оси x и подобным же образом использовать значения 
, то будет получена также не симметричная (но в другую сторону) формула (рис. 2.9.б):
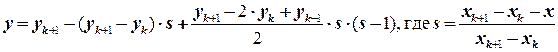
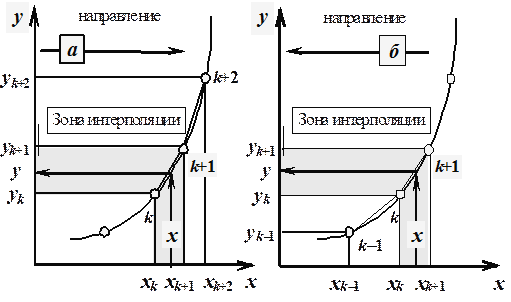
Рис. 2.9. Квадратичная интерполяция (метод Ньютона)
Взяв среднее арифметическое правых частей данных формул, получим симметричную формулу Бесселя, обладающую более высокой точностью:
