Случайная величина называется экспоненциально распределенной, если плотность ее вероятности (рис.4) 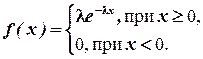
Рис. 2.4. Экспоненциальное распределение
Числоlназывается параметром распределения.
Длительность службы любого устройства можно рассматривать с хорошим приближением как экспоненциально распределенную величину.
2.1.2. Математическая статистика
Задача математической статистики состоит в том, чтобы на основании знания некотором свойств подмножества, взятых из некоторого множества, сделать какие-нибудь утверждения о свойствах этого множества, называемого генеральной совокупностью. В генеральной совокупности нас обычно интересует некоторый признак, который обусловленслучайностью и может иметь качественный или количественный характер.
Интересующий нас параметр некоторой генеральной совокупности может быть представлен в математической модели некоторой случайной величиной Х.
Под случайной выборкой объема n понимается выбор n объектов из генеральной совокупности, причем выбор отдельных объектов производится независимо (это обязательно) один от другого.
Результатом случайной выборки объема n является совокупность (х1,.,хn) значений признака.
Пусть (х1,...xn) -выборка. Вопрос о моделировании свойств данной выборки как случайной величины, которые можно было бы перенести на всю генеральную совокупность, является основным вопросом математической статистики.