Случайная величина называется распределенной нормально, если плотность вероятности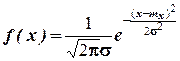 
, где mx и s параметры распределения. Функция f(x) представляет собой колоколообразную кривую (рис. 2.3).
Параметр mx – точка максимума, через которую проходит ось симметрии, параметр s – расстояние от этой точки до точки перегиба.
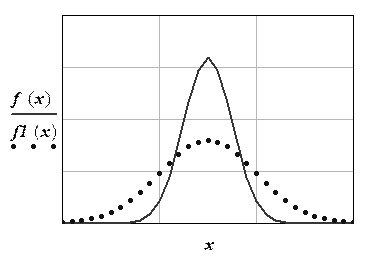
Рис. 2.3. Нормальное распределение (математическое ожидание для обоих распределений одинаковое, но разброс у кривой, показанной сплошной линией ниже, чем у показанной пунктирной линией)
Результат любого линейного или углового измерения можно рассматривать как нормально распределенную величину.
