П.4. Дробно-рациональные уравнения.

Определение.Уравнение, которое с помощь. равносильных преобразований можно привести к виду 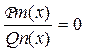, где Pm(x) и Qn(x) – многочлены соответственно m-й и n-й степеней, называется дробно рациональным уравнением.

Использование условия равенства нулю дроби приводит уравнение к системе: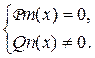

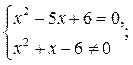
Например, 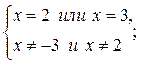х=3.

Ответ: 3.

Можно решение дробно-рациональных уравнений оформлять, опираясь на свойства равенств.

Примеры:

1) 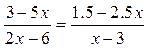.Умножим обе части уравнения на общий знаменатель дробей 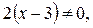получим целое уравнение 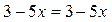, верное для любых . .

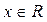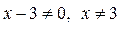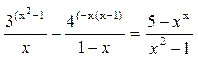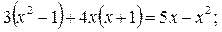
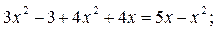
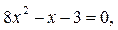
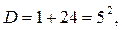
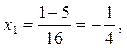
2) . Умножив обе части уравнения на общий знаменатель дробей (5), получим . х₁ и х₂ удовлетворяют условию (5). Ответ: .