Определение.Линейным называю уравнение, которое с помощью равносильных преобразований можно привести к виду 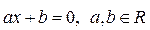 .
.
Алгоритм решения представим в виде схемы:
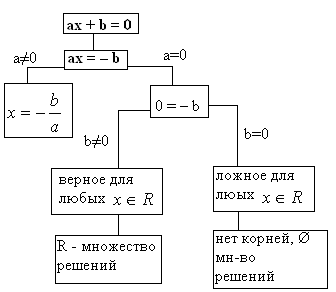
Если а ≠ 0, то уравнение имеет единственное решение 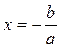 .
.
Если a=b=0, то R- множество решений.
Если а = 0, b≠ 0 то нет корней, т.е. Ø – множество решений.
Примеры.
1) 2х – 4 = 0, 2х = 4, х = 2. Ответ: 2.
2) 2x– 4 =2(x- 7), 2x– 4 = 2x– 14, 2x– 2x= -14 + 4, 0 ∙ x= 10– ложное для любыx 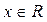 . Ответ: Ø.
. Ответ: Ø.
3) 2x– 14 = 2(x– 7), 2x– 14 = 2x– 14, 2x– 2x= 14 – 14, 0 = 0– верно для любых 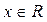 . Ответ: R.
. Ответ: R.
Решить уравнение 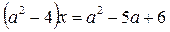 с параметром а.
с параметром а.
аможет принимать любое действительное значение. 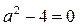 при
при 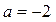 и при
и при 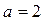 .
. 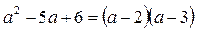 .
.
Если 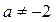 и
и 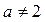 , то
, то 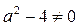 и
и 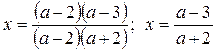 - один корень. Если
- один корень. Если 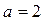 , то уравнение примет вид
, то уравнение примет вид 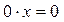 - верное числовое равенство при любых
- верное числовое равенство при любых 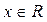 . Если
. Если 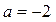 , то уравнение принимает вид
, то уравнение принимает вид  - ложное для любых
- ложное для любых 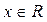 . Ответ:
. Ответ:  , если
, если 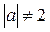 ; любое
; любое 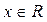 , если
, если 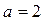 ; и нет решений, если
; и нет решений, если 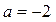 .
.