Над функциями можно совершать операции, одноименные с операциями: сложение, вычитание, умножение, деление, возведение в натуральную степень и другие. Например, пусть на множестве Х определены функции f(x) и g(x). Аналогично определяются и f– g, f·g, f:g.
Пусть f– взаимно однозначное отображение множества Х на множества У.
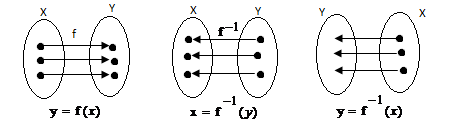
Если поменять местами образы и прообразы, то получим отображение 
, обратное данному отображению f. На графиках получается из fпростой сменой направления стрелок на противоположное и переименованием переменных.
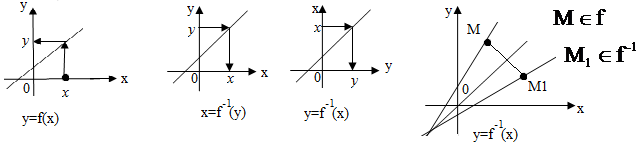На графике y=f(x) по значению аргумента х находят значение функции у (стрелка вертикально от х доходит до графика, затем поворачивает горизонтально до оси Оу). 
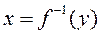описывает движения в обратном направлении от точки на оси Оу до точки на оси Ох. 
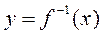получается после переименования осей Ох и Оу без изменения их расположения. При этих преобразованиях график не меняется. Наконец, располагая оси Ох и Оу привычен образом. Получаем график 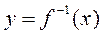с помощью симметричного отображения графика 
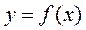относительно биссектрисы первого и третьего координатных углов у=х.
Если функция задана аналитически, то сначала формулу разрешают относительно х, затем переименовывают переменные. Например, у=3х-2 – данная функция.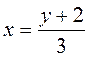 
– результат нахождения xчерез y. 
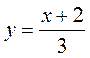- результат переименования переменных. Итак, для функции
