Операция возведения в степень определяет выражения с переменными трех видов в зависимости от того, какая из компонент содержит переменную: если основание степени содержит переменную, а показатель нет, то выражение называют степенным; если наоборот – то показательным; если и основание и показатель содержат переменные, то степень задает степенно-показательное выражение. Так,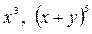 
– степенные выражения, 
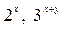– показательные выражения, 
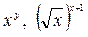– степенно-показательные.
Показательные выражения вида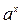 
имеет смысл рассматривать лишь при 
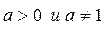, т.к. степень для произвольного 
определена только при 
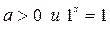. При 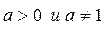выражение 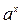устанавливает взаимно однозначное соответствие между множеством Rи 
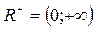, поэтому, обратные отношения тоже взаимно однозначно и задает отображение множества R+на множестве R, его называют операцией логарифмирования по основанию а.
Определение.Логарифмом положительного числа bпо основанию b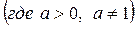 
называется показатель степени, в которую надо возвести а, что бы получить число b.
Символически: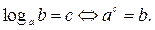 
Из определения следуют тождества:
1. 
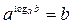(основное логарифмические тождество);
2. 
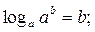
3. 
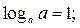
4. 
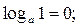
Из свойств степени и определения логарифма следуют свойства:
5. 
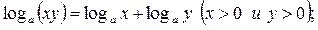
6. 
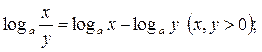
7. 
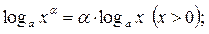
8. 
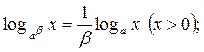
9. 
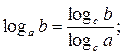
10. 
.
Докажем для примера свойства 5.
Пусть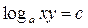 
, тогда 
. 
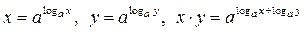, откуда следует, что 
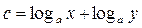и свойство 5.
Вводятся особые обозначение для десятичных (а=10) и натуральных (а=е, е≈2,7) логарифмов: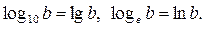 
Примеры.
1. 
, т.к.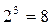 
;
2. 
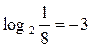, т.к. 
;
3. 
;
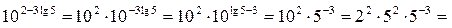
4. 
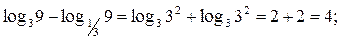
5. 
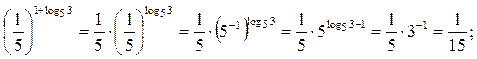
6. 
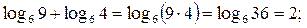
7. 
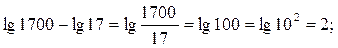
8. 
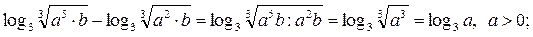
9. 
.
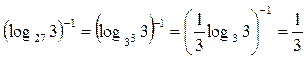