Ф. Блохом доказано, что волновые функции являются решением уравнения Шредингера с периодическим потенциалом, имеющим период решетки, представляют собой плоские волны, модулированные некоторой функцией с периодичностью решетки.
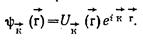- некоторая периодическая функция с периодом решетки, зависящая от длины волнового вектора k.
Условия периодичности потенциальной энергии электрона в кристалле
При смещении кристалла на вектор
, они совмещаются сами с собой. Из условия трансляционной симметрии следует, что волновая функция электрона отличается от волновой функции 
некоторым постоянным множителем
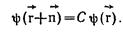
Из условия нормировки следует, что
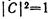
Этому можно удовлетворить, если предположить, что
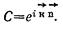
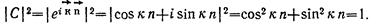
К - волновой вектор, характеризующий квантовое состояние электрона в кристале. Показатель степени экспоненты – безразмерная величина. Если - размерность длины, то к – размерность обратная длине, т.е. см-1. модуль вектора к является волновым числом. Физический смысл–число длин волн, укладывающихся на отрезке 2p.
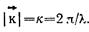
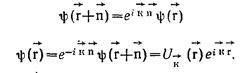
Здесь через
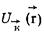обозначена функция
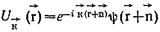
Являющаяся периодической с периодом решетки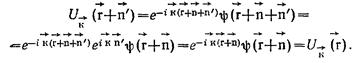 
Волновая функция электрона в кристалле представляет собой бегущую волну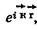 
, модулированную периодической функцией 
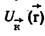, имеющей период решетки и зависящей от волнового вектора к.
Функция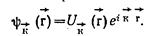 
называется функцией Блоха.
