Многоэлектронная задача может быть сведена к одноэлектронной методом Хартри – Фока, где потенциальная энергия взаимодействия электронов
заменяется потенциальной энергией вида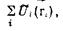 
, представляющей собой энергию взаимодействия i –го электрона с некоторым эффективным полем, в котором каждый электрон движется независимо. Это эффективное поле характеризует действие всех остальных электронов на i –й электрон, т.к. он оказывает воздействие на движение всех остальных электронов.
Под знаком суммы стоит гамильтониан i –го электрона
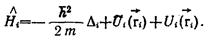
Уравнение Шредингера принимает вид
Т.к. гамильтониан не содержит энергии взаимодействия электронов и представляет собой сумму гамильтонианов отдельных электронов, решением уравнения является произведение одноэлектронных функций
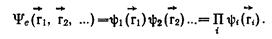
Каждая функция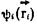 
удовлетворяет одноэлектронному уравнению Шредингера.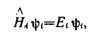 
В котором взаимодействие i –го электрона с остальными описывается потенциалом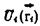 
Таким образом введение эффективного поля позволяет свести многоэлектронное уравнение к системе одноэлектронных. При этом энергия системы
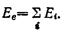
Волновая функция
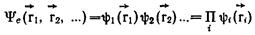
является решением уравнения Шредингера, но не удовлетворяет принципу Паули, по причине неудовлетворения функции
Антисимметричную функцию записывают в виде определителя Слэттера
Если обозначить потенциальную энергию через
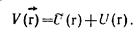
уравнение Шредингера имеет вид
является периодической функцией и ее период совпадает с периодом кристаллической решетки.
