Исправленный метод Эйлера.

В этом методе для повышения точности используется усреднённое значение производной на рассматриваемом отрезке:

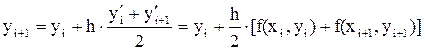
В приведённой формуле y_i+1 входит в обе части уравнения и не может быть выражено явно. Чтобы обойти эту трудность, в правую часть, вместо y_i+1 подставляется значение, рассчитанное по формуле Эйлера(7.4).

Получаем формулу исправленного метода Эйлера:

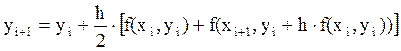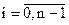, (7.7)

где i = 0, 1, …., n-1 - номер узла;

x_i = a + i×h - координата узла;

у₀ = у(х₀) - начальное условие.

Погрешность исправленного метода Эйлера d_М = О(h³).

Алгоритм решения ОДУ отличается от описанного ранее алгоритма метода Эйлера (рис 7.3) только алгоритмом расчета новой точки (Рис. 7.6).

Рис. 7.6. Алгоритм расчёта новой точки исправленным методом Эйлера:

L₁- касательная к у(х) в начальной точке А, с tga₀ = f(x₀, y₀).

т. В – значение 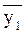вычисляется по формуле Эйлера.

L₂ – касательная к у(х) в точке В, с tga₁ = f(x₁, ).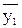

L₃ – прямая через В со среднеарифметическим углом наклона.

L₄ - прямая, паралельная L₃, проведенная через точку А.

Рис. 7.6. Геометрическая иллюстрация исправленного метода Эйлера.

Пример 7.3. Решение ранее рассмотренного уравнения (пример 7.1) исправленным методом Эйлера.

y^’ - 2×y + x² = 1, x Î [0;1], y(0) = 1.

Пусть n = 10 , h = (1 - 0)/10 = 0,1.

Начальная точка x₀ = 0, y₀ = 1.

Рассчет первой точки.

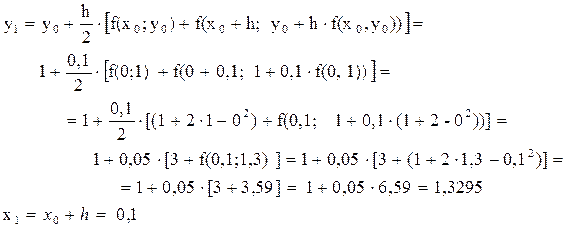
Аналогично можно вычислить значения функции во 2, 3, ... , 10 точках.