1) Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд (Теорема Дирихле. Переместительное свойство).
2) Абсолютно сходящиеся ряды с суммами 
можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна 
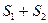(или соответственно 
).
3) Произведение двух абсолютно сходящихся рядов с суммами есть абсолютно сходящийся ряд с суммой 
. Под произведением двух рядов понимают ряд вида: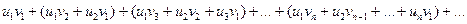 
Таким образом, абсолютно сходящиеся ряды суммируют, вычитают, перемножают как обычные ряды. Суммы таких рядов не зависят от порядка записи их членов.
В случае условно сходящихся рядов перечисленные свойства не имеют места. Поэтому действия над рядами нельзя производить. Не убедившись в их абсолютной сходимости. Для установления абсолютной сходимости используют все признаки сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем.
