Ряд, членами которого являются функции от х, называется функциональным: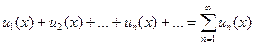 
(14.4)
Придавая х определенное значение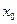 
, получаем числовой ряд:
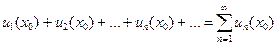(14.5). Этот ряд может сходиться или расходиться. Если полученный ряд сходится, то точка 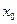называется точкой сходимости ряда (14.4), если же ряд расходится – точкой расходимости функционального ряда.
Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называется областью сходимости ряда.
В области сходимости функционального ряда его сумма является некоторой функцией от х: S=S(x). Определяется она в области сходимости равенством: 
.
Среди функциональных рядов особую роль играет ряд, членами которого являются степенные функции аргумента х, т.е. степенной ряд имеет вид: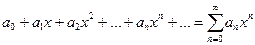 
(14.6),
где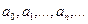 
- коэффициенты ряда действительные или комплексные числа,
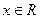- действительные переменные.
Степенной ряд, разложенный по степеням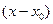 
,имеет вид:
(14.7),
где 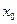- некоторое постоянное число.
Область сходимости степенного ряда содержит, по крайней мере, одну точку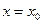 
Теорема Абеля. Сходимость степенных рядов.
Если степенной ряд сходится при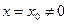 
, то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству 
.
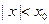Следствие: Если степенной ряд расходится при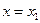 
, то он расходится и при всех х, удовлетворяющих неравенству 
.
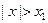