Знакочередующимся рядом называется ряд вида:
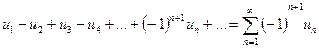(14.1).
.
Теорема. Достаточный признак сходимости знакочередующегося ряда. Признак Лейбница.
Знакочередующийся ряд (14.1) сходится, если:
1. Последовательность абсолютных величин членов ряда монотонно убывает, т.е. 
;
2. Общий член ряда стремится к нулю: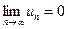 
.
При этом сумма S ряда (14.1) удовлетворяет неравенствам:
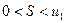. (14.2)
Замечания:
1) Исследование знакочередующегося ряда вида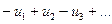 
(с отрицательным первым членом) сводится к исследованию ряда (14.1) путем умножения всех его членов на «-1»;
2) Соотношение (14.2) позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой 
. Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд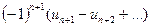 
, сумма которого по модулю меньше первого члена этого ряда, поэтому ошибка меньше чем модуль первого из отброшенных членов.
Теорема. Общий достаточный признак сходимости знакопеременных рядов.
Пусть дан знакопеременный ряд (2.3). Если сходится ряд, составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд (2.3).
Замечание: обратное утверждение несправедливо. Если сходится ряд (2.3), то это не означает, что будет сходиться ряд его модулей. Например, знакочередующийся ряд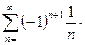 
сходится по признаку Лейбница, а ряд, составленный из модулей членов этого ряда. Расходится, так как он является гармоническим рядом.
