Пусть функция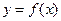 
непрерывна на промежутке 
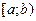и имеет разрыв II рода при x=b. Тогда несобственные интегралы от неограниченной функции определяются следующим образом:
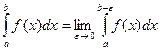(3.4)
Если предел, стоящий в правой части равенства (3.4) существует, то несобственный интеграл II рода называется сходящимся, в противном случае – расходящимся.
Аналогично, если функция 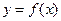имеет разрыв II рода в точке x=a, то полагают:
(3.5)
Если функция 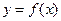имеет разрыв II рода во внутренней точке 
, то 
(3.6)
В этом случае интеграл называется сходящимся, если оба правые интегралы сходятся.
Существуют два признака сходимости и расходимости несобственных интегралов II рода:
1. Если на промежутке 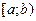функци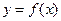и и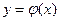 
непрерывны, при x=b имеют разрыв II рода и удовлетворяют условиям 
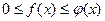, то из сходимости интеграла 
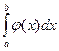следует сходимость интеграла 
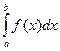, а из расходимости интеграла 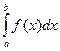следует расходимость интеграла .
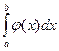2. Пусть на промежутке 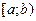функци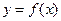и и 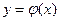непрерывны и при x=b имеют разрыв II рода. Если существует конечный предел 
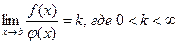, то интегралы 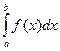и 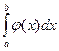сходятся или расходятся одновременно.
Примеры.
1) 
2) 
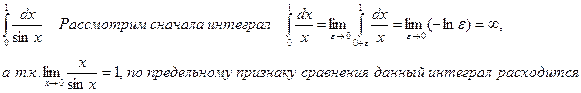
Лекция 13
