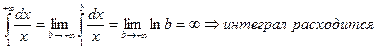Пусть функция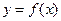 
интегрируема на любом отрезке 
. Тогда несобственные интегралы с бесконечными пределами интегрирования определяются следующим образом:
(3.1)
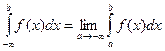(3.2)
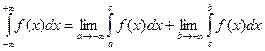(3.3), где с – произвольное число (обычно с=0).
Несобственные интегралы I рода называются сходящимися, если существуют конечные пределы, стоящие в правых частях формул (3.1), (3.2), (3.3). Если же указанные пределы не существуют или бесконечны, то несобственные интегралы называются расходящимися.
Существуют три признака сходимости и расходимости несобственных интегралов I рода:
1. Если на промежутке 
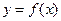непрерывные функции и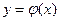 
удовлетворяют условиям 
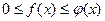, то из сходимости интеграла 
следует сходимость интеграла 
, а из расходимости интеграла следует расходимость интеграла . Этот признак называется признаком сравнения.
2. Если при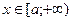 
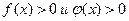и существует конечный предел 
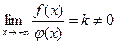, то интегралы и сходятся или расходятся одновременно. Этот признак называется предельным признаком сравнения.
3. Если сходится интеграл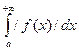 
, то сходится и интеграл , который в этом случае называется абсолютно сходящимся.
Примеры.
Выяснить, сходятся ли интегралы:
1) 
2) 
