Пусть функция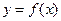 
определена, непрерывна и положительна на отрезке [a;b], где a<b. Фигура, ограниченная сверху графиком функции 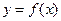, снизу - осью Ох, сбоку прямыми х=а и х=b называется криволинейной трапецией. Площадь этой криволинейной трапеции найдем, разделив отрезок [a;b] на частичные, как описано выше в 1.1. Составим интегральную сумму для этой функции на данном отрезке:
Каждое произведение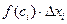 
представляет площадь прямоугольника со сторонами 
, а сумма площадей прямоугольников примерно равна площади криволинейной трапеции. Если n→∞, Sn→ S, где S – площадь криволинейной трапеции: 
.
Определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
