Рациональной дробью называется выражение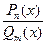 
, где 
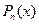и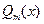 
- многочлены n-ой и m-ой степеней соответственно.
Рациональная дробь называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя: n<m.
Рациональная дробь называется неправильной, если степень многочлена числителя больше или равна степени многочлена знаменателя: 
.
Теорема. Всякую неправильную рациональную дробь можно представить в виде суммы многочлена (целой части) и правильной рациональной дроби путем деления числителя на знаменатель по правилу деления многочленов:
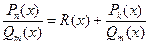, где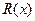 
- многочлен- частное, 
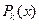- остаток (многочлен степени k<m).
Интегрирование рациональных дробей сводится к интегрированию многочлена R(x) и правильной дроби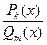 
:
Теорема. Всякую правильную рациональную дробь можно представить в виде суммы конечного числа простейших рациональных дробей четырех типов. Для этого необходимо многочлен знаменателя разложить на линейные и квадратные множители, найдя его корни, т.е.
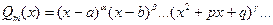, где 
- корни многочлена, 
, квадратные многочлены вида 
не имеют действительных корней.
Тогда правильную рациональную дробь 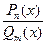можно единственным образом разложить на сумму простейших дробей:
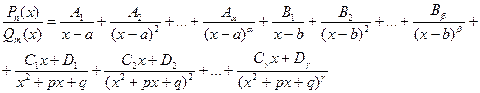, где
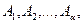
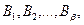
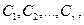
- некоторые действительные числа, которые находятся методом неопределенных коэффициентов или методом частных значений. Отметим, что общее число этих коэффициентов равно степени многочлена .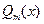
