Достаточно часто встречаются звенья, имеющие нелинейную зависимость между входной и выходной координатами. Если для малых отклонений от установившегося режима нелинейность несущественна, то в этом случае до составления исходных дифференциальных уравнений САУ выполняют процедуру линеаризации.
Линеаризацией называется замена реальных нелинейных уравнений статических характеристик элементов близкими к ним линейными уравнениями. Линеаризация возможна, если нелинейная характеристика непрерывна и имеет непрерывные частные производные. На рис.2.1. приведена геометрическая интерпретация линеаризации по методу малых отклонений.
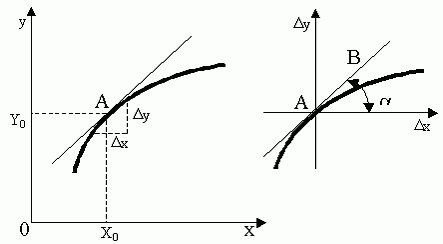
Рис.2.1. Геометрическая интерпретация линеаризации
Разложив функцию y=f(x) в ряд Тейлора, получим
где y0- значение выхода, соответствующее входу x0; dky/dxk - значения производных, взятых в точке А(x0;y0). Тогда для малых отклонений x:
или 
где 
при x=x0.
Если выходная величина элемента зависит от нескольких входных воздействий, то при линеаризации по методу малых приращений следует определять частные производные по всем воздействиям, а приращение вы-хода является суммой частных приращений, т.е.
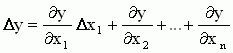
где x1, x2, …, xn - приращения входных воздействий;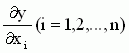 
- частные производные.
Пример задачи
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения.
