Рассмотрим квадратичную форму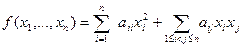 
+ 
для нахождения ее минимума в 
. Имеем
+ 
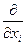
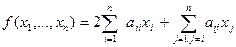= 0,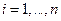 
.
Отсюда получаем следующую систему линейных алгебраических уравнений
= - , .
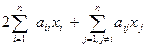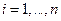Обозначим через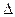 
определитель этой системы уравнений, через 
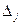- определитель 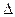, в котором вместо 
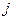- го столбца стоит столбец свободных членов. Тогда 
= ( 
,…, 
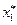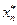), где 
= 
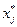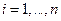, , является стационарной точкой. Матрица Гессе в данном конкретном случае имеет следующий вид 
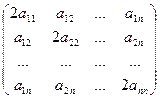. Является ли полученная стационарная точка экстремумом и максимумом или минимумом или не является точкой экстремума определяется в соответствии с п. 2.2.
