Рассмотримчастный случай кубической формы от двух переменных. Пусть 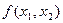 имеет следующий вид
имеет следующий вид
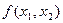 =
= 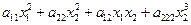 . (1)
. (1)
Имеем
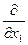
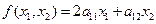 = 0, (2)
= 0, (2)
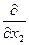
 = 0. (3)
= 0. (3)
Из (2) находим выражение 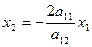 , подставляя которое в (3), получаем
, подставляя которое в (3), получаем
- 2 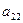
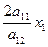 +
+ 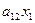 + 12
+ 12 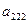 (
( 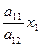
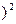 = 0,
= 0,
откуда получаем 2 решения: 1) 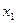 =
= 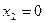 , 2)
, 2) 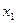 = (4
= (4 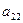
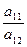 -
- 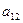 )(12
)(12 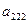
 (
( 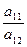
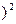
 ,
, 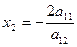 (4
(4 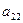
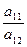 -
- 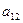 )(12
)(12 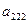 (
( 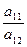
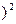
 . Итак, имеем две стационарные точки. Являются ли полученные стационарные точки экстремальными и максимумами или минимумами или не являются точками экстремума проверим в соответствии с п. 1.2 в зависимости от конкретных исходных данных. Матрица Гессе имеет следующий вид
. Итак, имеем две стационарные точки. Являются ли полученные стационарные точки экстремальными и максимумами или минимумами или не являются точками экстремума проверим в соответствии с п. 1.2 в зависимости от конкретных исходных данных. Матрица Гессе имеет следующий вид
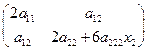 .
.
1. Рассмотрим случай решения 1: 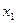 =
= 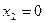 . В этом случае матрица Гессе имеет вид
. В этом случае матрица Гессе имеет вид
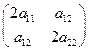 .
.
Если 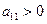 и
и 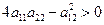 , то у
, то у 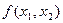 будет минимум. Если
будет минимум. Если 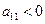
и 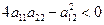 , то у
, то у 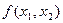 будет максимум. Во всех других случаях экстремума у
будет максимум. Во всех других случаях экстремума у 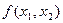 не будет.
не будет.
2. Рассмотрим случай решения 2: 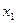 = (4
= (4 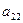
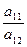 -
- 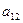 )(12
)(12 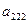
 (
( 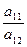
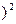
 ,
, 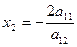 (4
(4 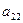
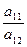 -
- 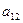 )(12
)(12 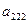 (
( 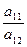
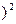
 . В этом случае матрица Гессе имеет вид
. В этом случае матрица Гессе имеет вид
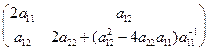 =
= 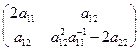 .
.
Если 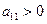 и
и  , то у
, то у 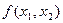 будет минимум. Если
будет минимум. Если 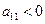
и 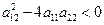 , то у
, то у 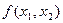 будет максимум. Во всех других случаях экстремума у
будет максимум. Во всех других случаях экстремума у 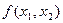 не будет.
не будет.
Заметим, что определитель матрицы Гессе в рассматриваемых двух стационарных точках отличается только знаком.