Сначала рассмотрим достаточные условия экстремума для функции двух переменных. Пусть в окрестности критической точки 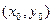 функция
функция 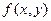 имеет непрерывные частные производные до второго порядка включительно. Рассмотрим определитель матрицы Гессе
имеет непрерывные частные производные до второго порядка включительно. Рассмотрим определитель матрицы Гессе
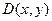 =
= 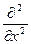
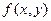

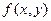 - (
- ( 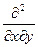
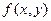 )
) 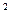 и
и 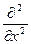
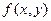
Если 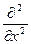
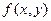
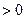 и
и  , то в точке
, то в точке 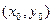
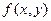 имеет минимум. Если
имеет минимум. Если 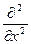
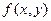
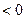 и
и 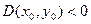 , то в точке
, то в точке 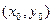
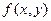 имеет максимум.
имеет максимум.
Достаточные условия экстремума для функции 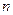 переменных. Если определитель матрицы Гессе и все главные миноры больше 0, то эта стационарная точка является минимумом
переменных. Если определитель матрицы Гессе и все главные миноры больше 0, то эта стационарная точка является минимумом 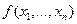 . Если ее определитель и все главные миноры меньше 0, то эта стационарная точка является максимумом
. Если ее определитель и все главные миноры меньше 0, то эта стационарная точка является максимумом 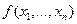 . Если ее определитель и главные миноры имеют разные знаки, то вышеуказанная стационарная точка не является экстремумом функции
. Если ее определитель и главные миноры имеют разные знаки, то вышеуказанная стационарная точка не является экстремумом функции 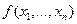 .
.
Главным минором 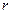 - го порядка матрицы называется минор, образованный её первыми
- го порядка матрицы называется минор, образованный её первыми 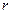 строками и
строками и 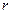 столбцами.
столбцами.
Рассмотрим последовательно случаи, когда возможно получение аналитического решения оптимальных задач без ограничений.