Определение. Функция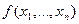 
называется сепарабельной, если она представляется в следующем виде: = 
+ 
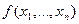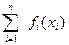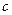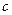, где - некоторая константа. Функции 
называются частными функциями.
Глобальный минимум сепарабельнойфункции достигается в точке минимума каждой из функций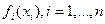 
, в силу независимости точки глобального минимума каждой из функций 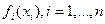, от точек глобального минимума остальных функций. Глобальный максимум сепарабельнойфункции достигается в точке глобального максимума каждой из функций 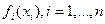, в силу независимости точки глобального максимума каждой из функций 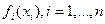, от точек глобального максимума остальных функций. Необходимыми и достаточными условиями того, что 
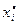-точка локального минимума 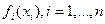, являются:
1) 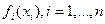, дифференцируема в точке ,
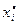2) 
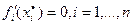, т.е. 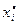является стационарной точкой,
3) 
.
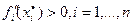Точка глобального минимума 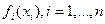, определяется перебором точек её локального минимума.
Необходимыми и достаточными условиями того, что 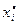-точка локального максимума 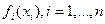, являются:
1) 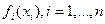, дифференцируема в точке ,
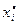2) 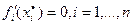, т.е. 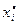является стационарной точкой,
3) 
.
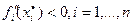Точка глобального максимума 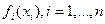, определяется перебором точек её локального максимума.
