Сформулируем постановку задачи: минимизировать функцию 
при отсутствии ограничений. Для задачи нелинейного программирования при отсутствии ограничений необходимыми условиями того, что 
- точка локального минимума, являются:
1) функцию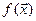 
дифференцируема в точке ,
2) 
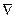
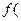
) = 0, т.е. существует стационарная точка в .
Достаточные условия того, что - точка локального минимума, кроме
приведенных условий 1) и 2) включает следующее:
3) 
) 
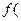
0, т.е. матрица Гессе положительно определенная.
Если 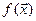- выпуклая функция при всех 
, 
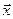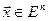, то необходимым и
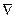
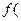
достаточным условием минимума является условие: ) = 0.
Процедура аналитического решения.
3. Проверяем выпуклость.
4. Если да, то решаем относительно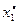 
,…, 
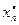систему уравнений
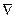
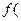
) = 0.
5. Если нет, то находим все множество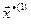 
,…, 
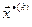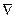
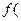
решений уравнений ) = 0.
6. Отбираем подмножество решений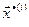 
, где 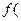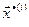) является выпуклой функцией. Если нет таких точек, значит решения нет.
Если есть, то из отобранных решений выбираем точку с наименьшим значением ).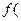
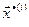В качестве примера рассмотрим случай целевой функции от двух переменных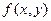 
. Если она в точке 
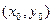имеет экстремум, то в этой точке либо ее частные производные первого порядка равны нулю, либо хотя бы одна из них не существует. Точка 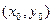называется критической (стационарной) точкой.
