Пусть функция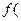 
) являетсястепенной функцией, умноженной на экспоненциальную функцию со степенью в виде полинома второй степени, т.е. ) = 
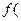
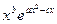. Имеем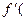 
) = 
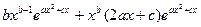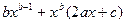= 0 
= 0 
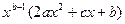= 0 , откуда определяются три конечные стационарные точки: 
, 
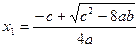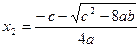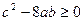при 
и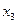 
= 0 при 
. Вторая производная 
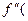
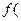
) от ) равна ) =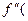 
( 
+ 
).
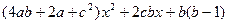Вторая производная 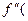) в точке 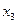= 0 равна 0 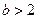при 
, при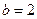 
неопределенна, при 
равна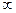 
, т.е. точка 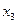= 0 не является точкой экстремума для ).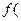
Поэтому остается рассмотреть возможные значения 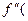) в точках = 
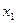и = 
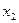. В зависимости от исходных данных 
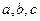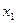корни и 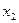могут принимать разные значения. Имеем следующие случаи:
1. 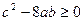. В этом случае 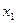и 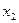являются действительными числами. Если )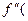 
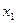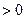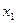, то является точкой минимума для функции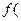 ). Если ) 
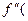
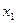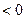, то 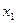является точкой максимума для функци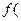и ). Если 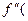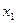) = 0, то 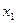не является точкой экстремума для функции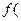 ). Эти же выводы справедливы и для точки .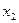
2. 
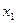. В этом случае и 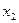являются комплексными числами и они не являются точками экстремума для функции ).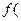
