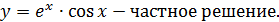Это дифференциальные уравнения вида:
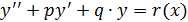
При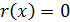 
получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
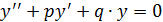
Для его решения составим характеристическое уравнение:
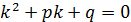
При его решении возможны следующие три случая:
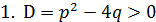
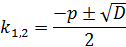
Общее решение дифференциального уравнения второго порядка находим по формуле:
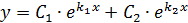
2. ЕслиD=0, то общее решение находится по формуле:
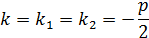
Тогдаобщее решение дифференциального уравнения находим по формуле:
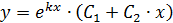
3. 
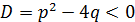, то корни комплексно - сопряженные.
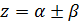
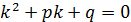
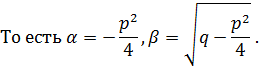
Тогда общее решение находится по формуле:
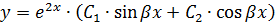
Пример 1.
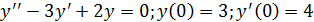
Решение:
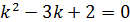
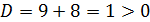
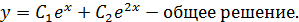
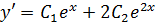
При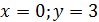 
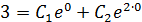
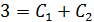
При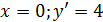 
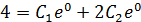
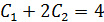
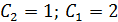
Ответ: 
Пример 2.
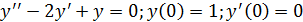
Решение:
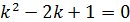
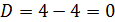
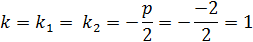
2 способ:
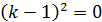
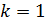
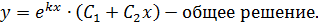
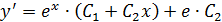
При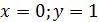 
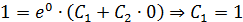
При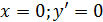 
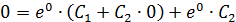
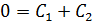
Ответ: 
Пример 3.
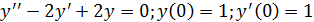
Решение:
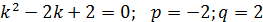
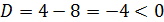
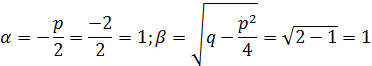
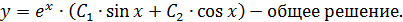
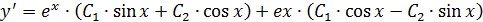
При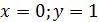
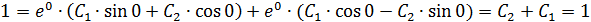
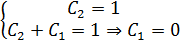
Ответ: 
