Иногда решение дифференциальных уравнений второго порядка можно свести к последовательному решению двух дифференциальных уравненийпервого порядка. Тогда говорят, что дифференциальное уравнение допускает понижение порядка.
Это дифференциальные уравнения вида:
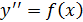
или
Пример 1.
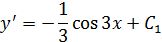
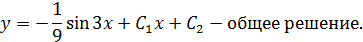
Пример 2.
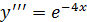
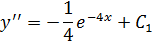
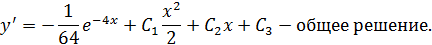
Уравнения этого типа решаются заменой переменной 
Следовательно,
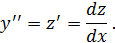
Подставим в дифференциальное уравнение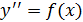 
.
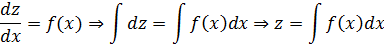
Подставив значение zв дифференциальное уравнение 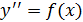, найдем функцию y.
Пример.
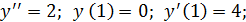
Решение:
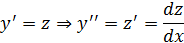
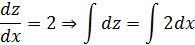
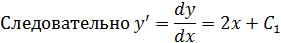
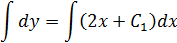
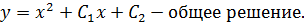
Так как при x= 1, y = 0 и при x = 1, 
, то
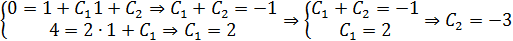
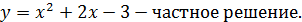
Ответ: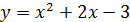 
.
