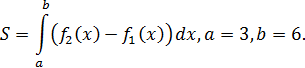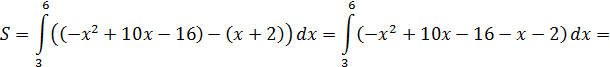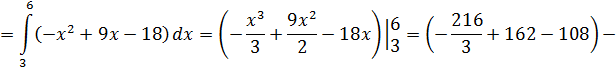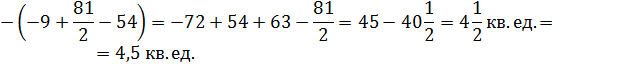Геометрический смысл определенного интеграла.
Определенным интегралом от функции f (x) на промежутке [a; b] называется предел интегральной суммы(1).
Геометрический смысл.
Определенный интеграл от непрерывной неотрицательной функции
f(x) на промежутке [a; b] численно равен площади соответствующей криволинейной трапеции:
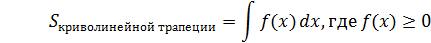
Геометрические приложения определенного интеграла.
1. Вычисление Sфигуры.
1) Если геометрическая фигура ограничена графиками двух непрерывных неотрицательных функций 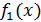 и
и 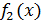 .
.
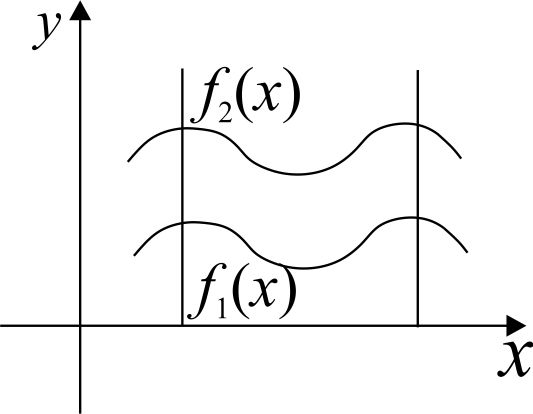
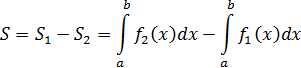
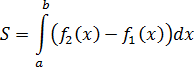
2) Если геометрическая фигура ограничена графиком 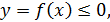
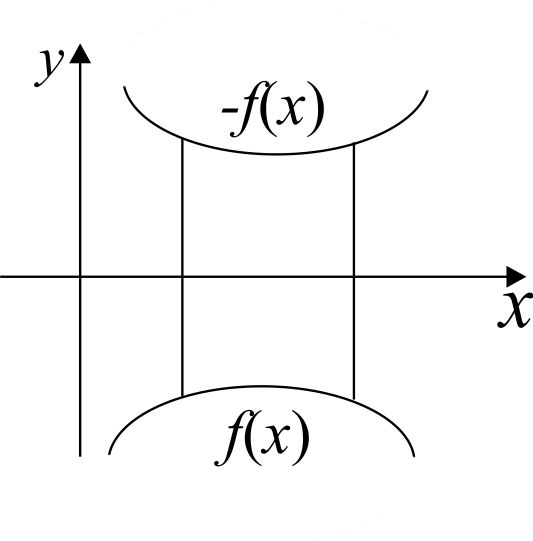
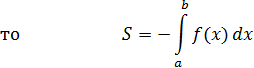
3) Если 

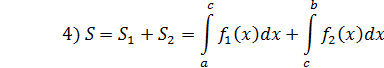
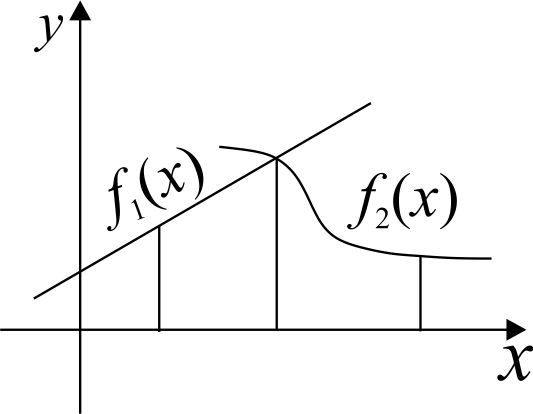
Пример.
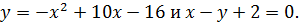
Решение:
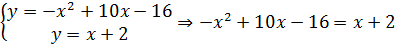
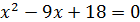
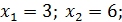
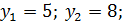
(3; 5), (6; 8) ‒ точки пересечения линии.


Второйспособ:
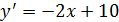
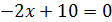


(5; 9) ‒ вершина параболы.