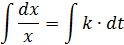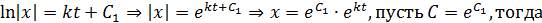Лекция 13. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

.

Задачи, приводящие к дифференциальным уравнениям.

1. Задача о нахождении закона движения материальной точки.

Обозначив 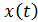‒ путь в момент времени , ‒скорость, тогда из физического смысла производной следует, что

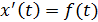
или

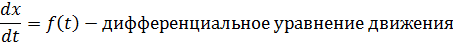
Если 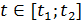, то получим , проинтегрировав это равенство, получим закон движения:

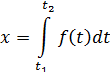
2. Задача о размножении бактерий.

Пусть ‒ число бактерий в момент времени .Так как скорость размножения бактерий пропорциональна их количеству, то по аналогии с предыдущим.

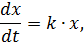
где 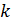‒ коэффициент пропорциональности.