Связь показательного распределения с процессом Пуассона

Пусть в СМО требования поступают в случайные моменты времени t_o = 0, t₁, t₂,..., так что u_k = t_k - t_k-1 (k ≥ 1) – интервалы между поступлениями и, кроме того,

.

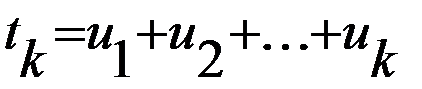Предположим, что случайные величины u₁,u₂,...,u_k независимы и имеют показательное распределение с параметром λ:

Другими словами, входной поток требований в систему является простейшим.

Пусть ν(t) - число требований, поступивших в СМО в интервале времени (0, t). Тогда справедлива формула

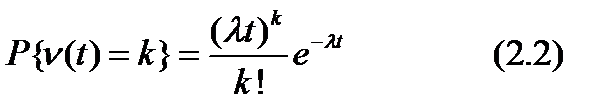
означающая, что если длительности промежутков между поступлениями в систему последовательных требований имеют показательный закон, то случайное число требований, поступивших за время t, имеет распределение Пуассона с параметром , а процесс ν(t) является однородным пуассоновским процессом.

Имеет место и обратное: если число требований ν(t), поступивших за время t, является процессом Пуассона с интенсивностью λ, то длительности интервалов u_k независимы и имеют одинаковое показательное распределение с параметром λ.