Для систем с ожиданием время ожидания растет с увеличением числа требований. Имеет место простое соотношение, связывающее среднее число требований Q, находящихся в системе, интенсивность входного потока λ, и среднее время пребывания требования в системе Т:
Это соотношение называется формулой Литтла. Таким образом, среднее число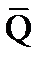 
требований в СМО равно произведению интенсивности поступления требований в систему на среднее брела пребывания требования в системе.
Формулу (1.1) можно отнести как ко всей системе, состоящей из очереди и обслуживающего прибора, так и только к очереди требований. Во втором случае формула Литтла примет вид
где 
- среднее число требований в очереди, a 
- среднее время ожидания в очереди.
Применяя соотношение (1.1) к СМО, состоящей только из обслуживающего прибора (или приборов), получаем третью формулу Литтла
где s - среднее число требований, находящихся на обслуживании, а 
- среднее время обслуживания одного требования. Отметим, что всегда имеет место равенство
Лекция №2
