Определим работу источника тока, которую он должен совершить, чтобы в контуре с индуктивностью 
создать ток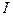 
. Работа источника, по перемещению заряда 
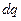против ЭДС индукции равна: 
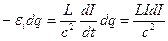. Она же равна увеличению энергии магнитного поля контура при увеличении в нем тока на 
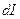. Полную энергию магнитного поля контура с током 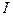получим после интегрирования:
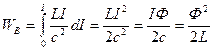. (21.1)
В частности, энергия магнитного поля в куске безграничного соленоида длиной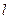 
будет равна:
.
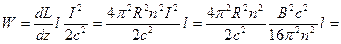
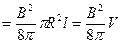В преобразованиях мы использовали результаты 20.3 и 16.6. Окончательный результат дает нам энергию однородного магнитного поля в объеме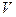 
. Используя его, можем определить объемную плотность энергии магнитного поля:
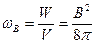. (21.2)
В случае неоднородного магнитного поля его энергия в любом объеме может быть найдена интегрированием по этому объему:
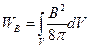. (21.3)
Энергетические соотношения могут быть использованы и для нахождения индуктивностей проводников. Покажем это на третьем примере, рассмотренном в предыдущем параграфе.
Определяем энергию магнитного поля на единицу длины коаксиального кабеля, а затем и индуктивность единицы длины:
.
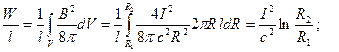
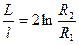Получили тот же результат, что и при использовании для вывода выражения (20.2).
